Угловые скорости на круговых орбитах зависят от радиуса по закону Ньютона:
, будет иметь радиус:
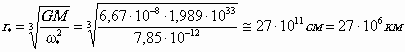
Все планеты, имеющие радиус круговой орбиты > 
, будут получать от
Солнца момент количества движения и удаляться от него, если бы
масса Солнца оставалась постоянной. Это результат воздействия
приливных волн на Солнце.
Все тела и малые планеты, которые были и есть на орбитах с радиусом менее 27 млн. км должны были приливными волнами тормозиться и падать на Солнце. При этом момент количества движения Солнца будет возрастать.
Тот факт, что экваториальная угловая скорость вращения Солнца больше скорости в полярных областях, можно рассматривать как свидетельство непрерывного потока падающих на Солнце тел. Полярные области получают свою долю момента количества движения только за счет выравнивания угловых скоростей в объеме Солнца. Количественная оценка этого взаимодействия кажется невозможной без поступающей массы из Космоса через полярные области.
Для подобных оценок важны и предположения о глубинном строении Солнца, в том числе, о величине ядра. Возможно и повторяющиеся выбросы плазмы являются следствием не внутренних процессов, а падения космических тел, захваченных Солнцем.
Гравитационное взаимодействие двух тел конечного размера обусловлено их взаимным притяжением. Эти силы приложены к центру масс каждого тела и направлены по линии, соединяющей эти центры.
Силы инерции, удерживающие тела от падения друг на друга, связаны с движением по криволинейным траекториям и направлены так, чтобы в каждый момент уравновешивать силы тяготения. Центр масс двух тел остается неподвижным. Форма отдельного тела определяется собственным гравитационным полем, распределением массы в объеме тела и его способностью удерживать свою первоначальную форму силами сцепления между своими частями тела на разных масштабных уровнях.
Если тело вращается около собственной оси, то действие сил инерции также не может быть уравновешенным в объеме тела без участия сил сцепления. При взаимодействии двух тел их собственные гравитационные поля постоянно находятся в возмущенном состоянии, что вызывает непрерывное движение масс внутри тел. Это движение изменяет форму тел и влияет на движение тел друг относительно друга вследствие обмена моментом количества движения.
Возмущенные собственные гравитационные поля могут быть представлены эквипотенциальными поверхностями, что бывает удобно при рассмотрении осесимметричных тел. Эквипотенциальная поверхность возмущенного поля тесно связана со взаимным расположением двух тел, а само тело вращается вокруг собственной оси. В каждый момент времени эквипотенциальная поверхность показывала бы ту форму, которую должно принять физическое тело, чтобы действие гравитации двух тел было скомпенсировано на поверхности. Очевидно, что это равновесие недостижимо: ускорение пропорционально расстоянию между поверхностями и будет убывать со временем.
Постоянство скорости вращения тела в неподвижном возмущенном собственном гравитационном поле должно привести к устойчивому профилю поверхностной волны, которая движется вслед за фазой максимального отклонения от эквипотенциальной поверхности. Скорость поверхностных волн зависит от длины волны, Это позволяет выделить ту длину волны, которая будет определять амплитуду деформации поверхности тела.
Поверхностные волны связаны с перемещением масс лишь вблизи поверхности в слое, соизмеримом с длиной волны. Можно ожидать, что регулярно повторяющееся механическое движение в слое постоянной толщины должно наделить его свойствами, отличными от соседних слоев.
В атмосфере с непрерывно меняющейся плотность по высоте (по радиусу) определить положение относительно тонкого слоя, рожденного приливными волнами, затруднительно.
Введем дополнительно следующее соображение. В слое, где механическое движение обусловлено приливными поверхностными волнами, непрерывно повышается кинетическая энергия атомов и растет соответственно скорость звуковых волн. Если эта часть механической энергии не будет ограничена, то газодинамические волны конечной амплитуды рассеют энергию приливной волны. Это будет происходить до тех пор, пока слой не займет положение, где энергетический баланс не ограничит скорость звуковых волн на пределе, равном скорости движения приливной волны в гравитационном поле.
Можно догадаться, что на Солнце этим условиям удовлетворяет фотосфера, интенсивно излучающая свет.
Пусть фотосфера тот слой, по которому движется приливная волна.
Скорость волны в тонком слое равна 
, где g – ускорение силы тяжести на
поверхности Солнца, 
-
толщина фотосферы. Скорость приливных волн определяется в основном
угловой скоростью вращения Солнца. Умножая ее на радиус, получим:
. Постоянная g=2,7
104 см/с2 , 
= 1,7 105 см/с.
Отсюда следует: =106
см или 10 км.
Скорость звуковых волн в фотосфере не должна превышать скорость
приливных волн с=1,7 105 см/с. Если бы фотосфера имела
тот же молекулярный состав, что и тропосфера, где скорость
приливных волн и скорость звука равны, их температуры относились
бы как квадраты скорости звука. Это отношение равно 30, и
температура фотосферы должна бы равняться ~ 90000 К.
Если фотосфера состоит из газа того же состава в атомарном
состоянии, то температура ее будет в 
раза меньше, т.е. ~ 50000 К
Разумеется эти количественные оценки температуры не имеют доказательной силы, но они наводят на размышление о роли механического взаимодействия планет и Солнца. Разогрев фотосферы приливными волнами и перемещение этого тонкого слоя по глубине, а также изменение скорости вращения Солнца – все это может влиять на излучаемые Солнцем световые потоки и на жизнь на Земле.
Представляется необходимым критически пересмотреть общепринятые представления об энергоисточниках эволюционных процессов в солнечной системе и в недрах планет.