В.Н.Родионов

Механическое движение в мантии Земли и свойства мантийной среды

1. Неоднородная по плотности мантия в поле силы тяжести не может находиться в состоянии статического равновесия. Наличие тяжелого ядра и относительно легкой литосферы свидетельствуют о уже прошедшей дифференциации вещества в недрах Земли. Нет основания полагать, что этот процесс закончился. Более того, всплывание легких объемов в мантии и погружение тяжелых – это главный движитель эволюции нашей планеты.

Действие силы тяжести направлено к центру Земли и распространяется на все материальные частицы, где бы они ни находились, независимо от их окружения. Но движение частиц или отдельных частей физического тела зависит от местоположения и контактов с ближайшим окружением. Энергия частиц или частей тела зависит от величины и направления скорости движения, так как сила тяжести может изменять энергию только у движущихся частиц.

Механические свойства деформируемых тел определяются запасом внутренней энергии и взаимоотношением его частей, начиная с молекулярного уровня. В твердых телах первостепенное значение приобретают надмолекулярные структуры, существующие за счет энергии макродвижения или гравитационных полей. По этой причине объяснение необычных механических, вернее, физических свойств мантии невозможно без рассмотрения характера и структуры перемещения тяжелых и легких объемов в ее среде.

2. Напомним привычные характеристики твердого тела в механике. Признаком твердого тела является сопротивление его формоизменению. Внешние силы, приложенные к телу, деформируют тело и порождают в нем внутренние напряжения, которые уравновешивают действие внешних сил. В упругом теле эти напряжения однозначно связаны с деформациями и после разгрузки тела от внешних сил напряжения исчезают и форма тела восстанавливается. Однако такое поведение упругого тела имеет место лишь при малых деформациях, когда относительное увеличение расстояния между произвольными точками не превышает 10^-3 . При больших деформациях твердое тело разрушается или становится неупругим. Вследствие малости упругих деформаций связь их с напряжениями с достаточной для инженерной практики точностью можно считать линейной. Упругое тело Гука стало моделью твердого деформируемого тела в механике.

Неупругие пластические деформации и дезинтеграция (разделение тела на отдельные куски) у всех реальных твердых тел происходят при относительно низких средних напряжениях в теле. Если оценивать разрывающие материал напряжения через силу связи атомов, то можно получить величины на три порядка превышающие опытные значения. Объяснение этому было найдено в деформации структур реальных тел: равновесные трещины Грифитса и дислокации в кристаллических решетках. Исследование разрушения материалов, в частности, те, которые проводились в Ленинградском Физтехе, обнаруживали существенное влияние на механические свойства твердых тел всевозможных надмолекулярных структур. Прямым свидетельством неоднородности реальных твердых тел является поглощение в них энергии упругих колебаний и волн.

Большое разнообразие твердых тел, созданных природой и человеком, нуждалось в модельном представлении их деформационных свойств, Необходимо. было учесть роль неоднородностей при деформировании.

3. Модель твердого тела с неоднородностями в общих чертах выглядит следующим образом. В линейно упругом теле равномерно по объему распределены неоднородности различного размера, около которых при деформировании упругого тела возникают избыточные напряжения сдвига, релаксирующие во времени. В таком теле внешние силы, деформирующие тело, уравновешиваются напряжениями упругого тела и напряжениями на неоднородностях. Релаксация напряжений является свойством физического тела, а скорость деформации определяется действием внешних сил. Вследствие этого сопротивление деформированию оказывается зависящим от скорости деформирования.

Время релаксации напряжения на каждой неоднородности зависит от ее размера. В модели твердого тела вводится для всех материалов и горных пород одна скорость релаксации 2.10^-6 см/с, так что время релаксации увеличивается линейно с размерами неоднородности. Отсюда следует, что при заданной скорости деформирования сопротивление действию внешних сил окажут не все неоднородности. На мелких неоднородностях избыточные напряжения будут малы вследствие их релаксации. Присутствие очень крупных неоднородностей также остается малозаметным, так как релаксация напряжений на них будет весьма продолжительной.

Чтобы сопоставить силу напряжений на неоднородностях с упругими напряжениями в твердом теле, нужно их проинтегрировать в заданном сечении и отнести к площади. Полученную таким образом величину будем называть неупругими напряжениями.

Каждая скорость деформирования вызывает активную реакцию лишь у тех неоднородностей, размер которых находится вблизи величины, определяемой отношением скорости релаксации и скорости деформации. Более крупные и более мелкие неоднородности остаются в этом случае пассивными. Объем всех неоднородностей одного размера обычно не превышает 0.01 объема твердого тела. Того же порядка будет вклад неупругих напряжений в сопротивление действию внешних сил.

В задачах о статическом равновесии, если процесс нагружения был кратковременным, неупругие напряжения себя не обнаруживают. Однако в динамических процессах, где возникают длительные колебания в твердых телах, с неупругими напряжениями связано и поглощение энергии колебаний и появление зародышей усталостных трещин.

Еще более значимы неупругие напряжения при чрезвычайно медленном деформировании, что типично для твердых тел в земных недрах. Концентрация неоднородностей разного размера, начиная с дефектов кристаллических решеток, достигает таких значений, при которых суммарный объем релаксирующих неоднородностей становится соизмеримым с объемом твердого тела. Упругие области, разделенные зонами релаксирующих неоднородностей, уже не могут сопротивляться сдвиговым деформациям тела и упругие напряжения выключаются полностью. С этого момента деформирование прежде твердого тела связано исключительно с неупругими напряжениями. Механические свойства тела при этом изменяются качественно. Деформация сдвига в таком теле осуществляется путем смещения частиц разного размера, разделенных зонами релаксации. Величина перемещения и деформация больше не являются определяющими параметрами, они могут расти неограниченно, не влияя на силу сопротивления.

Если выделить поверхность смещения одной части тела относительно другой, то напряжения сдвига на этой границе (будь то поверхность скольжения или имеющая конечную толщину зона) изменяются пропорционально скорости смещения. Твердое тело становится похоже на вязкую жидкость.

В случае остановки движения напряжения уменьшаются до нуля, так что для возобновления движения достаточно сколь угодно слабых усилий. Вместе с тем сцепление частей тела может восстановиться до прочности монолита с прекращением релаксационных процессов при сохранении неподвижности.

Переходные процессы "разжижения" твердого тела с появлением многочисленных зон релаксации и процессы отвердения занимают конечные интервалы времени, которые зависят от размеров тела и неоднородностей в нем. Хотя это напоминает плавление и кристаллизацию твердых тел, важно отметить различия: температура и молекулярные тепловые движения в рассмотренном примере никакой роли не играют. Что касается подобия, то оно требует специального рассмотрения

4. В неоднородной по плотности мантии под действием силы тяжести должно возникать и поддерживаться движение разномасштабных объемных структур. Можно внести некоторую определенность в описание динамических структур, построив модель неоднородного по плотности твердого тела. Составим тело из равного числа легких и тяжелых кубиков, случайным образом располагая их в теле. Все кубики имеют одинаковые размеры, а плотность материала как легких, так и тяжелых кубиков в своей группе также одинакова. В таком теле произвольно выбранные объемы кубической формы из 8 кубиков будут представлены 256-ю вариантами укладок. Разобьем все укладки на три группы: легкие, средние и тяжелые. Границы между ними установим так, чтобы средние составили половину, а легкие и тяжелые четверть общего числа кубиков. Изготовим кубики с ребром в два раза большим, чем у первичных кубиков, присвоим половине среднюю плотность, четверти одинаковую избыточную плотность и другой четверти плотность меньшую средней. Усредним плотности по группам, получим три сорта кубиков. Отклонение от среднего значения у легких и тяжелых кубиков одинаково.

Теперь уже из этих кубиков будем составлять твердое тело, а затем все варианты укладок объемов из восьми кубиков снова распределим по группам: легкие, средние и тяжелые. Далее процедура повторяется. При таком распределении всех вариантов укладок на три группы обнаруживается, что отличие плотности легких объемов и тяжелых от среднего с ростом их объема уменьшается, как и следовало ожидать. Но теперь модель позволяет выявить количественную зависимость. Пусть объем первоначальных кубиков L₀ . Кубические объемы в соответствии с принятой процедурой укладки и осреднения по группам имеют размеры

Отличие от средней плотности легких и тяжелых объемов

Эта модель неоднородного по плотности твердого тела предложена для мантии. Средняя плотность мантийного вещества известна. В качестве крайних значений плотности составных ее частей могут быть взяты плотности на границе с ядром и у поверхности Земли. Очевидно, что в любой смеси частиц разной плотности, объемы, превосходящие первичные частицы, будут иметь в большинстве случаев среднюю плотность смеси. Имея в виду выявить роль силы тяжести в формировании подвижных объемов, следовало избегать каких либо сложных смесей, сохраняющих свою специфику на разных масштабных уровнях. Модель, составленная из 2-х видов кубиков, показала, что закономерность выравнивания плотностей с возрастанием объемов усреднения не зависит от размеров первичных кубиков. Использование кубиков в качестве элементов сплошной среды оказалось удобным для получения количественных соотношений из уравнения равновесия сил.

В поле силы тяжести легкие объемы всплывают, а тяжелые тонут. Применительно к кубическому объему составим уравнение равновесия сил. Необходимым условием действия сил Архимеда является попадание легкого (тяжелого) объема в окружение из объемов со средней плотностью. С кубическим объемом контактируют шесть таких же объемов. по границе. Обозначим сопротивление движению по границе через равнение равновесия сил:

Сила сопротивления пропорциональна скорости относительного движения v.

Преобразуя уравнение равновесия сил для блока L_k с учетом зависимости от размера L_k , полученной на модели тела неоднородного по плотности, получим:

Сокращая Lк в левой и правой части уравнения, имеем:

Произведение характеризует начальную неоднородность твердого тела: L^* - тот минимальный размер объема, в пределах которого отличие плотности от среднего значения имеет максимальное значение. Это произведение определяет скорость всплытия и погружения объемов в мантии.

Независимость уравнения силового равновесия от L_к означает, что все объемы

L_k = 2^k L^* будут двигаться с одинаковой скоростью.

В рассмотренной модели неоднородного по плотности тела весь спектр разномасштабных легких и тяжелых объемов формируется вследствие перемешивания без разрушения целостности исходных тяжелых и легких кубиков. В мантии нашей планеты теперь отыскать характеристики первичной плотностной неоднородности трудно. Поэтому будем рассматривать L^* и как условное обозначения неоднородностей плотности.

Примем = 1 г/см³ и определим L^* для различных значений скоростей движения легких и тяжелых объемов. Будем считать g = 10³ см/с², а = 1. Если скорость измерять в см/год, то

Максимальное значение возможной скорости всплытия или погружения обусловлено дезинтеграцией сплошного материала в зонах интенсивного смещения объемов относительно друг друга, где не успевают релаксировать упругие напряжения. Эта скорость по порядку величины равна 10 см/год. При достижении этой скорости всплывающий и тонущий объемы формируют локальные поверхности скольжения, где перемалываются островки упругой среды. В результате движущийся объем обособляется от окружающей среды и может долго сохранять свою скорость и плотность.

При движении со скоростями меньше предельной легкие и тяжелые объемы имеют неограниченные возможности обмениваться веществом с окружающей средой и поэтому существуют в течение времени прохождения пути, равного их размеру. Попадая в новое окружение с иными распределениями плотностных неоднородностей движущийся объем теряет скорость, а процесс разделения легких и тяжелых частиц продолжат вновь возникшие в других местах легкие и тяжелые движущиеся объемы.

В соответствии с уравнением равновесия сил линейный размер объема, средняя плотность которого отличается от средней плотности мантии на 1 г/см³ , при v = 10 см/год равен L^* = 600 м. Пользуясь формулой L_k = 2^k L^* , определим линейные размеры L₁ = 1200 м, L₂ = 2400 м и L₃ = 4800 м. Отличие от средней плотности мантии будут у этих объемов:

Все эти объемы будут двигаться со скоростью 10 см/год; легкие всплывая, тяжелые погружаясь. Эти долгоживущие движущиеся объемы с устойчивыми границами можно назвать уже телами. Их слабый обмен массой с окружающей средой позволяет им всплывать или погружаться на тысячи километров.

Вероятность образования такого объекта равна произведению вероятностей существования заданного объема с повышенной (или пониженной) плотностью и появления в его окружении 6 объемов того же размера со средней плотностью: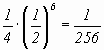

При такой вероятности их существования тела легкие и тяжелые не будут взаимодействовать и встречные потоки одинаковых по размеру тел не будут замечать друг друга. Тоже самое можно сказать о всех 4-х телах разного размера. Каждое тело в соответствии с указанной вероятностью занимает 1/256 часть пространства, а все вместе 1/256х4х2 = 1/32 объема мантии.

Движение легких и тяжелых объемов со скоростями менее 10 см/год имеет как было сказано пульсирующий характер. Движущиеся объемы имеют короткую жизнь и непостоянный вещественный состав из-за обмена с окружающей средой. Их масштабы ничем не регламентированы. Распределим все движущиеся объемы на три группы по скорости:v = 5 см/год; v = 2,5 см/год; v = 1,25 см/год. Масштабный параметр L^* для этих групп будет соответственно равен: 300 м; 150 м и 75 м. Для каждого масштаба плотностной неоднородности выделим первые четыре размера (L^*, 2L^*, 4L^*, 8L^*) легких и тяжелых объемов. Всего получим 3х4х2 = 24 объема с отличной от среднего значения плотностью. Каждый объем занимает 1/256 часть мантии. Все эти объемы вместе с ближайшим окружением (х7) соизмеримы с объемом мантии:

Пульсирующее перемещение легких и тяжелых объемов охватывает всю мантию.

5. Модель твердого тела, неоднородного по плотности в поле силы тяжести, демонстрирует переход всего тела в состояние всеобщего движения разномасштабных объемов внутри тела. Пульсирующее движение возникающих и распадающихся ассоциаций под действием сил Архимеда плавно перемещает тяжелые и легкие частицы в противоположные стороны, мало изменяя объем тела как целого и не производя существенных структурно-плотностных изменений. Это стационарное состояние, питаемое за счет энергии гравитационного поля, рождает сплошную среду с необычными механическими свойствами, которые определяются надмолекулярными структурами. На макромасштабном уровне в такой среде можно заметить признаки одновременно твердого и жидкого тела: распространение упругих волн и текучесть при ничтожных нагрузках.

Питание энергией движущихся объемов за счет гравитационного поля осуществляется вследствие все проникающей его способности непосредственно по месту и в момент перемещения в количестве, пропорциональном скорости. Такое индивидуальное питание разрешает всевозможные локальные преобразования как свойств среды, так и форм движения. Так, например, выключение на продолжительное время из всеобщего движения некоторого объема приведет к его твердению, к восстановлению высокой прочности.

Можно представить и противоположный эффект, когда некоторая часть поверхности слоя мантии без видимых внешних воздействий сама приобретет текучесть..

Возможно, многие образы, предложенные для толкования поведения физических тел, контролируемых на молекулярном уровне, можно использовать и для описания физических тел в мантии. Однако в макромасштабе, как нами показано, это создает неоправданные трудности в правильном толковании результатов наблюдений.